[암호학] 비대칭키 암호 - ElGamal (공개키 암호시스템)

ElGamal 방식
1. 개요
- ElGamal은 이산대수 문제의 어려움에 근거해서 만든 시스템이다.
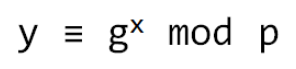
- 이산대수의 문제의 어려움이란, p가 소수이고 g가 원시원소일 때 g, x, p를 이용하여 y=g^x mod p 를 구하긴 쉽지만 g,y,p 값을 이용하여 지수승의 x를 구하기는 어렵다는 것이다.
- 이 때문에 ElGamal 암호에서는 x가 개인키, y가 공개키로 사용된다.
- ElGamal은 디지털 서명, 암호화, 키 교환에 사용될 수 있는 공개키 알고리즘이다.
- ElGamal은 실제로 Diffie-Hellman 알고리즘의 확장이다.
- ElGamal의 주요한 결점은 성능이다. 다른 알고리즘과 비교할 때 가장 느리다.
※ 이산대수 문제 예

2. 암호화와 복호화
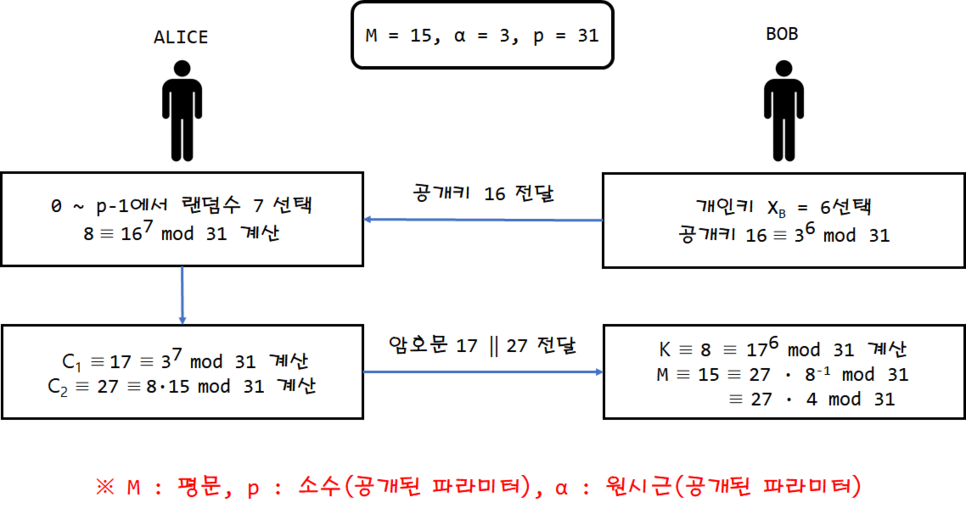
◆ Alice가 BOB 에게 암호문을 보내려고 하는 경우

① BOB이 개인키와 공개키를 만든다.
★ 2와 p-2 사이의 정수를 고르는 이유
실제로 사용할 수 있는 키의 개수는 1 ~ p - 1까지 사용할 수 있지만 다음과 같은 이유 때문에 제외됩니다.
▶ 개인키가 1일 경우 : 공개키가 원시원소가 되고 이를 통해 개인키를 유추할 수 때문에 안전성에 문제가 있습니다.(원시원소는 공개되기 때문)
▶ 개인키가 p - 1일 경우 : p - 1을 제곱할 경우 나머지가 1이 되기 때문입니다. 즉, 공개키가 1이 되고 위와 마찬가지로 개인키를 유추할 수 있습니다.
② ALICE가 BOB에게 받은 공개키로 K를 만든다.
▶ r는 0부터 p-1 사이의 랜덤 수입니다.
▶ r이 랜덤 수이기 때문에 암호화를 할 때마다 다른 K 값이 나와 같은 평문이라도 다른 암호문이 나오게 됩니다.
③ ALICE는 최종 암호문인 C를 생성한다.
▶ C1 : BOB이 K 값을 BOB의 개인키로 알 수 있게 하는 암호문이며 r을 공개할 수 없기 때문에 이와 같은 암호문으로 보냅니다.
▶ C2 : 실질적인 암호문. 평문과 K를 곱해 p로 나눈 나머지 값입니다.
④ BOB이 자신의 개인키로 K를 얻고 암호문을 복호화 한다.
▶ 자신의 개인키(XB)로 C1을 복호화 하여 K를 얻습니다.
▶ K로 C1을 나눠 p로 나눈 나머지 값을 구하여 암호문으로부터 평문을 얻습니다.
※ K 값을 얻을 수 있는 이유
ALICE가 생성한 K 값 : K ≡ (YB)r mod p ≡ (αXB)r mod p
BOB이 획득한 K 값 : K ≡ (C1)XB mod p ≡ (αr)XB mod p
Elgamal 암호 예시
Elgamal 암호 예시 ▶ 마지막 복호화 하는 부분에서 8을 나눠줘야 하기 때문에 8-1을 곱해줬습니다.
★ 8-1이 4가 된 이유
확장된 유클리드 알고리즘을 사용해줘도 되지만 여기선 p가 소수이기 때문에 오일러 법칙을 사용하는 것이 더 간단합니다.
1 ≡ ap - 1 mod p를 오일러 법칙이라고 합니다.
즉, 대입을 하게 되면 1 ≡ 831 - 1 mod 31가 됩니다.
하지만 저희가 구하고 싶은 값은 8-1입니다.
그래서 양변에 8-1을 곱하게 되면 8-1 ≡ 8-1 · 831 - 1 mod 31 가 되고
8-1 ≡ 831 - 2 mod 31 ≡ 829 mod 31 이 됩니다.
이것을 계산해주면 4가 됨을 알 수 있습니다.
아래의 식을 보시면 더 쉽게 이해하실 수 있습니다.
오일러의 법칙 출처: Bin@ry_W0r1d 네이버 블로그
3. 특징
- 같은 평문이라도 암호화가 이루어질 떄마다 암호문이 달라진다.
- ElGamal 암호계에서는 암호문 전달 과정에서 알 수 있듯이 평문이 암호문으로 될 때 순서쌍으로 표현되므로 이 암호계에서 암호문의 길이는 평문의 약 2배가 된다.
- RSA 암호와 비교하여 그만큼 많은 메모리 공간이 필요하며 전송 속도 또한 지체되는 단점을 가지고 있다. 최근 이산대수 문제에 대한 연구가 발전됨에 따라 소수 p의 크기는 768비트 이상의 수를 사용하도록 권고하고 있다.
4. 응용
- ElGamal은 RSA를 활용할 수 있는 곳에는 어디에나 사용할 수 있다. 키 교환, 인증, 짧은 메시지의 암호화와 복호화에 사용할 수 있다.
- 암호 소프트웨어 GnuPG에 구현되어 있다.